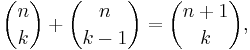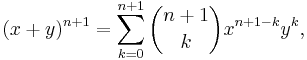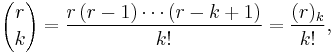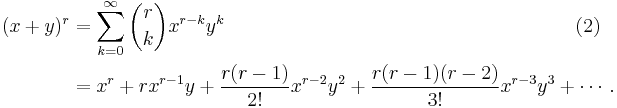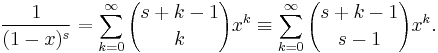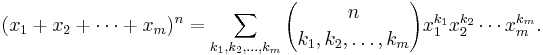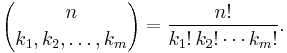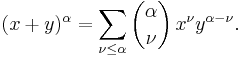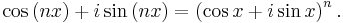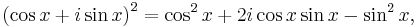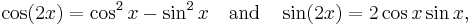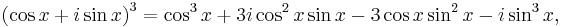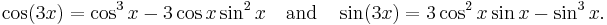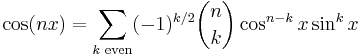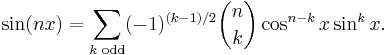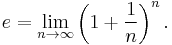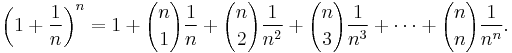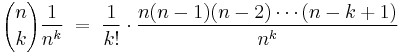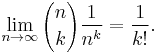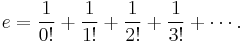Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power (x + y)n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with b + c = n, and the coefficient a of each term is a specific positive integer depending on n and b. When an exponent is zero, the corresponding power is usually omitted from the term. For example,
The coefficient a in the term of xbyc is known as the binomial coefficient 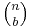 or
or 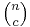 (the two have the same value). These coefficients for varying n and b can be arranged to form Pascal's triangle. These numbers also arise in combinatorics, where
(the two have the same value). These coefficients for varying n and b can be arranged to form Pascal's triangle. These numbers also arise in combinatorics, where 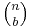 gives the number of different combinations of b elements that can be chosen from an n-element set.
gives the number of different combinations of b elements that can be chosen from an n-element set.
Contents |
History
This formula and the triangular arrangement of the binomial coefficients are often attributed to Blaise Pascal, who described them in the 17th century, but they were known to many mathematicians who preceded him. The 4th century B.C. Greek mathematician Euclid mentioned the special case of the binomial theorem for exponent 2[1][2] as did the 3rd century B.C. Indian mathematician Pingala to higher orders. A more general binomial theorem and the so-called "Pascal's triangle" were known in the 10th-century A.D. to Indian mathematician Halayudha and Persian mathematician Al-Karaji,[3], in the 11th century to Persian poet and mathematician Omar Khayyam[4], and in the 13th century to Chinese mathematician Yang Hui, who all derived similar results.[5] Al-Karaji also provided a mathematical proof of both the binomial theorem and Pascal's triangle, using mathematical induction.[3]
Statement of the theorem
According to the theorem, it is possible to expand any power of x + y into a sum of the form
where each 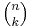 is a specific positive integer known as binomial coefficient. This formula is also referred to as the Binomial Formula or the Binomial Identity. Using summation notation, it can be written as
is a specific positive integer known as binomial coefficient. This formula is also referred to as the Binomial Formula or the Binomial Identity. Using summation notation, it can be written as
The final expression follows from the previous one by the symmetry of x and y in the first expression, and by comparison it follows that the sequence of binomial coefficients in the formula is symmetrical.
A variant of the binomial formula is obtained by substituting 1 for x and x for y, so that it involves only a single variable. In this form, the formula reads
or equivalently
Examples
The most basic example of the binomial theorem is the formula for the square of x + y:
The binomial coefficients 1, 2, 1 appearing in this expansion correspond to the third row of Pascal's triangle. The coefficients of higher powers of x + y correspond to later rows of the triangle:
Notice that
- the powers of x go down until it reaches 0 (
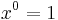 ),starting value is n (the n in
),starting value is n (the n in 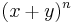 .)
.) - the powers of y go up from 0 (
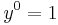 ) until it reaches n (also the n in
) until it reaches n (also the n in 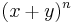 .)
.) - the nth row of the Pascal's Triangle will be the coefficients of the expanded binomial.(Note that the top is row 0.)
- the number of products is equal to
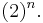
- the number of product groups is equal to
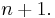
The binomial theorem can be applied to the powers of any binomial. For example,
For a binomial involving subtraction, the theorem can be applied as long as the opposite of the second term is used. This has the effect of changing the sign of every other term in the expansion:
Geometric explanation
For positive values of a and b, the binomial theorem with n = 2 is the geometrically evident fact that a square of side a + b can be cut into a square of side a, a square of side b, and two rectangles with sides a and b. With n = 3, the theorem states that a cube of side a + b can be cut into a cube of side a, a cube of side b, three a×a×b rectangular boxes, and three a×b×b rectangular boxes.
In calculus, this picture also gives a geometric proof of the derivative 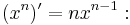 [6] if one sets
[6] if one sets 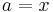 and
and 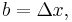 interpreting b as an infinitesimal change in a, then this picture shows the infinitesimal change in the volume of an n-dimensional hypercube,
interpreting b as an infinitesimal change in a, then this picture shows the infinitesimal change in the volume of an n-dimensional hypercube, 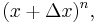 where the coefficient of the linear term (in
where the coefficient of the linear term (in 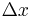 ) is
) is 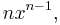 the area of the n faces, each of dimension
the area of the n faces, each of dimension 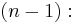
Substituting this into the definition of the derivative via a difference quotient and taking limits means that the higher order terms – 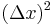 and higher – become negligible, and yields the formula
and higher – become negligible, and yields the formula 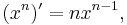 interpreted as
interpreted as
- "the infinitesimal change in volume of an n-cube as side length varies is the area of n of its
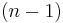 -dimensional faces".
-dimensional faces".
If one integrates this picture, which corresponds to applying the fundamental theorem of calculus, one obtains Cavalieri's quadrature formula, the integral 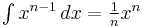 – see proof of Cavalieri's quadrature formula for details.[6]
– see proof of Cavalieri's quadrature formula for details.[6]
The binomial coefficients
The coefficients that appear in the binomial expansion are called binomial coefficients. These are usually written 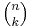 , and pronounced “n choose k”.
, and pronounced “n choose k”.
Formulas
The coefficient of xn−kyk is given by the formula
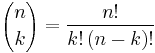 ,
,
which is defined in terms of the factorial function n!. Equivalently, this formula can be written
with k factors in both the numerator and denominator of the fraction. Note that, although this formula involves a fraction, the binomial coefficient 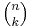 is actually an integer.
is actually an integer.
Combinatorial interpretation
The binomial coefficient 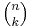 can be interpreted as the number of ways to choose k elements from an n-element set. This is related to binomials for the following reason: if we write (x + y)n as a product
can be interpreted as the number of ways to choose k elements from an n-element set. This is related to binomials for the following reason: if we write (x + y)n as a product
then, according to the distributive law, there will be one term in the expansion for each choice of either x or y from each of the binomials of the product. For example, there will only be one term xn, corresponding to choosing 'x from each binomial. However, there will be several terms of the form xn−2y2, one for each way of choosing exactly two binomials to contribute a y. Therefore, after combining like terms, the coefficient of xn−2y2 will be equal to the number of ways to choose exactly 2 elements from an n-element set.
Proofs
Combinatorial proof
Example
The coefficient of xy2 in
equals 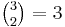 because there are three x,y strings of length 3 with exactly two y's, namely,
because there are three x,y strings of length 3 with exactly two y's, namely,
corresponding to the three 2-element subsets of { 1, 2, 3 }, namely,
where each subset specifies the positions of the y in a corresponding string.
General case
Expanding (x + y)n yields the sum of the 2 n products of the form e1e2 ... e n where each e i is x or y. Rearranging factors shows that each product equals xn−kyk for some k between 0 and n. For a given k, the following are proved equal in succession:
- the number of copies of xn − kyk in the expansion
- the number of n-character x,y strings having y in exactly k positions
- the number of k-element subsets of { 1, 2, ..., n}
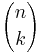 (this is either by definition, or by a short combinatorial argument if one is defining
(this is either by definition, or by a short combinatorial argument if one is defining 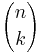 as
as 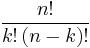 ).
).
This proves the binomial theorem.
Inductive proof
Induction yields another proof of the binomial theorem (1). When n = 0, both sides equal 1, since x0 = 1 for all nonzero x and 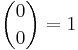 . Now suppose that (1) holds for a given n; we will prove it for n + 1. For j, k ≥ 0, let [ƒ(x, y)] jk denote the coefficient of xjyk in the polynomial ƒ(x, y). By the inductive hypothesis, (x + y)n is a polynomial in x and y such that [(x + y)n] jk is
. Now suppose that (1) holds for a given n; we will prove it for n + 1. For j, k ≥ 0, let [ƒ(x, y)] jk denote the coefficient of xjyk in the polynomial ƒ(x, y). By the inductive hypothesis, (x + y)n is a polynomial in x and y such that [(x + y)n] jk is 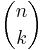 if j + k = n, and 0 otherwise. The identity
if j + k = n, and 0 otherwise. The identity
shows that (x + y)n+1 also is a polynomial in x and y, and
If j + k = n + 1, then (j − 1) + k = n and j + (k − 1) = n, so the right hand side is
by Pascal's identity. On the other hand, if j +k ≠ n + 1, then (j – 1) + k ≠ n and j +(k – 1) ≠ n, so we get 0 + 0 = 0. Thus
which is the inductive hypothesis with n + 1 substituted for n and so completes the inductive step.
Generalisations
Newton's generalised binomial theorem
Around 1665, Isaac Newton generalised the formula to allow real exponents other than nonnegative integers, and in fact it can be generalised further, to complex exponents. In this generalisation, the finite sum is replaced by an infinite series. In order to do this one needs to give meaning to binomial coefficients with an arbitrary upper index, which cannot be done using the above formula with factorials; however factoring out (n−k)! from numerator and denominator in that formula, and replacing n by r which now stands for an arbitrary number, one can define
where 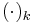 is the Pochhammer symbol here standing for a falling factorial. Then, if x and y are real numbers with |x| > |y|,[7] and r is any complex number, one has
is the Pochhammer symbol here standing for a falling factorial. Then, if x and y are real numbers with |x| > |y|,[7] and r is any complex number, one has
When r is a nonnegative integer, the binomial coefficients for k > r are zero, so (2) specializes to (1), and there are at most r + 1 nonzero terms. For other values of r, the series (2) has infinitely many nonzero terms, at least if x and y are nonzero.
This is important when one is working with infinite series and would like to represent them in terms of generalised hypergeometric functions.
Taking r = −s leads to a useful but non-obvious formula:
Further specializing to s = 1 yields the geometric series formula.
Generalisations
Formula (2) can be generalised to the case where x and y are complex numbers. For this version, one should assume |x| > |y|[7] and define the powers of x + y and x using a holomorphic branch of log defined on an open disk of radius |x| centered at x.
Formula (2) is valid also for elements x and y of a Banach algebra as long as xy = yx, x is invertible, and ||y/x|| < 1.
The multinomial theorem
The binomial theorem can be generalised to include powers of sums with more than two terms. The general version is
where the summation is taken over all sequences of nonnegative integer indices k1 through km such that the sum of all ki is n. (For each term in the expansion, the exponents must add up to n). The coefficients 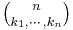 are known as multinomial coefficients, and can be computed by the formula
are known as multinomial coefficients, and can be computed by the formula
Combinatorially, the multinomial coefficient 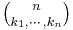 counts the number of different ways to partition an n-element set into disjoint subsets of sizes k1, ..., kn.
counts the number of different ways to partition an n-element set into disjoint subsets of sizes k1, ..., kn.
The multi-binomial theorem
It is often useful when working in more dimensions, to deal with products of binomial expressions. By the binomial theorem this is equal to
- Failed to parse (unknown function\dotsm): (x_{1}+y_{1})^{n_{1}}\dotsm(x_{d}+y_{d})^{n_{d}} = \sum_{k_{1}=0}^{n_{1}}\dotsm\sum_{k_{d}=0}^{n_{d}} \binom{n_{1}}{k_{1}}\, x_{1}^{k_{1}}y_{1}^{n_{1}-k_{1}}\;\dotsc\;\binom{n_{d}}{k_{d}}\, x_{d}^{k_{d}}y_{d}^{n_{d}-k_{d}}.
This may be written more concisely, by multi-index notation, as
Applications
Multiple angle identities
For the complex numbers the binomial theorem can be combined with De Moivre's formula to yield multiple-angle formulas for the sine and cosine. According to De Moivre's formula,
Using the binomial theorem, the expression on the right can be expanded, and then the real and imaginary parts can be taken to yield formulas for cos(nx) and sin(nx). For example, since
De Moivre's formula tells us that
which are the usual double-angle identities. Similarly, since
De Moivre's formula yields
In general,
and
Series for e
The number e is often defined by the formula
Applying the binomial theorem to this expression yields the usual infinite series for e. In particular:
The kth term of this sum is
As n → ∞, the rational expression on the right approaches one, and therefore
This indicates that e can be written as a series:
Indeed, since each term of the binomial expansion is an increasing function of n, it follows from the monotone convergence theorem for series that the sum of this infinite series is equal to e.
The binomial theorem in abstract algebra
Formula (1) is valid more generally for any elements x and y of a semiring satisfying xy = yx. The theorem is true even more generally: alternativity suffices in place of associativity.
The binomial theorem can be stated by saying that the polynomial sequence { 1, x, x2, x3, ... } is of binomial type.
See also
- Binomial distribution
- Binomial probability
- Binomial inverse theorem
- Binomial series
- Combination
- Stirling's approximation
- Multinomial theorem
- Negative binomial distribution
- Pascal's triangle
- Binomial approximation
Notes
- ^ Binomial Theorem
- ^ The Story of the Binomial Theorem, by J. L. Coolidge, The American Mathematical Monthly 56:3 (1949), pp. 147–157
- ^ a b O'Connor, John J.; Robertson, Edmund F., "Abu Bekr ibn Muhammad ibn al-Husayn Al-Karaji", MacTutor History of Mathematics archive, University of St Andrews, http://www-history.mcs.st-andrews.ac.uk/Biographies/Al-Karaji.html.
- ^ Sandler, Stanley (2011). An Introduction to Applied Statistical Thermodynamics. Hoboken NJ: John Wiley & Sons, Inc.. ISBN 978-0-470-91347-5.
- ^ Landau, James A (1999-05-08). "Historia Matematica Mailing List Archive: Re: [HM] Pascal's Triangle" (mailing list email). Archives of Historia Matematica. http://archives.math.utk.edu/hypermail/historia/may99/0073.html. Retrieved 2007-04-13.
- ^ a b (Barth 2004)
- ^ a b This is to guarantee convergence. Depending on r, the series may also converge sometimes when |x| = |y|.
References
- Bag, Amulya Kumar (1966). "Binomial theorem in ancient India". Indian J. History Sci 1 (1): 68–74.
- Barth, Nils R. (November 2004). "Computing Cavalieri's Quadrature Formula by a Symmetry of the n-Cube". The American Mathematical Monthly (Mathematical Association of America) 111 (9): 811–813. doi:10.2307/4145193. ISSN 0002-9890. JSTOR 4145193, author's copy, further remarks and resources
- Graham, Ronald; Donald Knuth, Oren Patashnik (1994). "(5) Binomial Coefficients". Concrete Mathematics (2nd ed.). Addison Wesley. pp. 153–256. ISBN 0-201-55802-5. OCLC 17649857.
- Solomentsev, E.D. (2001), "Newton binomial", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=n/n066500
External links
- Binomial Theorem by Stephen Wolfram, and "Binomial Theorem (Step-by-Step)" by Bruce Colletti and Jeff Bryant, Wolfram Demonstrations Project, 2007.
- Binomial Theorem Introduction
This article incorporates material from inductive proof of binomial theorem on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
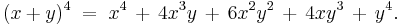
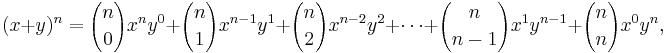
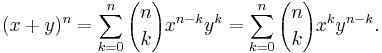
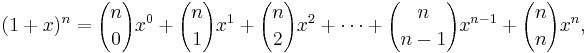
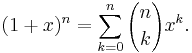
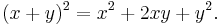
![\begin{align}
(x%2By)^3 & = x^3 %2B 3x^2y %2B 3xy^2 %2B y^3, \\[8pt]
(x%2By)^4 & = x^4 %2B 4x^3y %2B 6x^2y^2 %2B 4xy^3 %2B y^4, \\[8pt]
(x%2By)^5 & = x^5 %2B 5x^4y %2B 10x^3y^2 %2B 10x^2y^3 %2B 5xy^4 %2B y^5, \\[8pt]
(x%2By)^6 & = x^6 %2B 6x^5y %2B 15x^4y^2 %2B 20x^3y^3 %2B 15x^2y^4 %2B 6xy^5 %2B y^6, \\[8pt]
(x%2By)^7 & = x^7 %2B 7x^6y %2B 21x^5y^2 %2B 35x^4y^3 %2B 35x^3y^4 %2B 21x^2y^5 %2B 7xy^6 %2B y^7.
\end{align}](/2012-wikipedia_en_all_nopic_01_2012/I/05912cb66ba1a0cc47688071d5cdae8a.png)
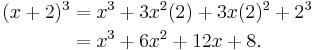
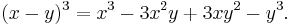
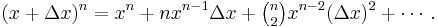
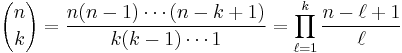
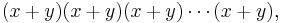
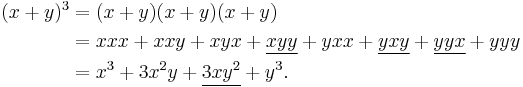
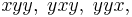
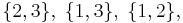
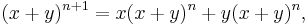
![[(x%2By)^{n%2B1}]_{jk} = [(x%2By)^n]_{j-1,k} %2B [(x%2By)^n]_{j,k-1}. \,](/2012-wikipedia_en_all_nopic_01_2012/I/7e1705a0868645bb42809f3cb58980de.png)